Question

A mixture of CH4 and H2O is passed over a nickel catalyst at 1000 K. The emerging gas is collected in a 5.00-L flask and is found to contain 8.62 g of CO, 2.60 g of H2, 43.0 g of CH4, and 48.4 g of H2O.

Answer 1

The given question is incomplete. But the complete question is this:

A mixture of
`CH_(4)` and
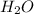`H_2O` is passed over a nickel catalyst at 1000 K. The emerging gas is collected in a 5.00-L flask and is found to contain 8.62 g of CO, 2.60 g of
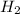`H_2`, 43.0 g of
`CH_(4)`, and 48.4 g of
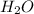`H_(2)O`. Assuming that equilibrium has been reached, calculate
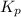`K_(p)` for the reaction.

Step-by-step explanation:

As the given reaction is as follows.

`CH_4 + H_2O \rightarrow CO + 3H_2`

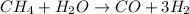
And, we know that

No. of moles =
`\frac{mass}{\text{molar mass}}`

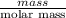
Therefore, calculate the moles as follows.

Moles of
`CH_4` =
`(43)/(16.04)`

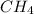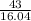
= 2.6808 mol

Moles of
`H_2O` =
`(48.4)/(18.01528)`

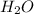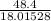
= 2.6866 mol

Moles of CO =
`(8.62)/(28.01)`

= 0.307747 mol

Moles of
`H_(2)` =
`(2.6)/(2.01588)`

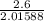
= 1.2897 mol

As, we know that

Concentration =
`(moles)/(volume (L) )`

Given volume = 5 L

Hence, calculate the concentration of given species as follows.

Conc. of
`CH_4 = (2.6875)/(5)`

= 0.5361

Conc. of
`H_2O = (2.6889)/(5)`

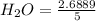
= 0.5373

Conc. of CO =
`(0.307747)/(5)`

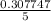
= 0.06155

and, Conc. of
`H_2 = (1.2897)/(5)`

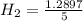
= 0.2579

Now, expression for equilibrium constant for the given reaction is as follows.

`K_(c) = ([CO][H_2]^(3))/([CH_4][H_2O] )`

Now, putting the given values into the above formula as follows.

`K_(c) = ([0.06155][0.2579]^(3))/([0.5361][0.5373])`

`K_(c) = 3.665 * 10^(-3)`

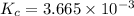
Also, we know that

`K_p = K_c * (RT)^dn`

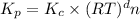
Consider the equation

`CH_4(g) + H2O(g) \rightarrow CO(g) + 3H_2(g)`

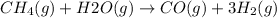
Calculate change in moles of gas as follows.

change in gas moles (dn) = 1 + 3 - 1 - 1

dn = 2

As,
`K_p = K_c * (RT)^2`

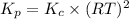
It is given that,

T = 1000 K , R = 0.0821

So,

`K_p = 3.665 * 10^(-3) * (0.0821 * 1000)^(2)`

`K_p` = 24.70

Thus, we can conclude that value of
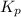`K_(p)` for the reaction is 24.70.