Answer
given,
length of rod = 21.5 cm = 0.215 m
mass of rod (m) = 1.2 Kg
radius, r = 1.50
mass of ball, M = 2 Kg
radius of ball, r = 6.90/2 = 3.45 cm = 0.0345 m
considering the rod is thin
![I = (1)/(3)M_(rod)L^2 + [(2)/(5)M_(ball)R^2+M_(ball)(R+L)^2]](https://img.qammunity.org/2020/formulas/physics/high-school/xcwswj2cp2d5xd1k66x6no3ni1zb91lmbr.png)
![I = (1)/(3)* 1.2 * 0.215^2 + [(2)/(5)* 2 * 0.0345^2+2* (0.0345 +0.215)^2]](https://img.qammunity.org/2020/formulas/physics/high-school/gxvpsxqutptubaqtkevywxjgmtlk2rwar7.png)
I = 0.144 kg.m²
rotational kinetic energy of the rod is equal to
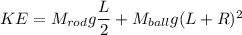
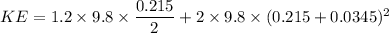
KE = 6.15 J
b) using conservation of energy
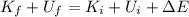
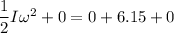
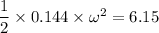
ω = 9.25 rad/s
c) linear speed of the ball
v = r ω
v = (L+R )ω
v = (0.215+0.0345) x 9.25
v =2.31 m/s
d) using equation of motion
v² = u² + 2 g h
v² = 0 + 2 x 9.8 x 0.248
v = √4.86
v =2.20 m/s
speed attained by the swing is more than free fall
% greater =
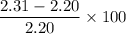
= 5 %
speed of swing is 5 % more than free fall