Answer:
Explanation:
Plot that point in the x/y coordinate plane to see that it sits in the third quadrant. From the point, draw a line to the origin, constructing a right triangle. The side adjacent to the angle is -2, the side across from the angle is -5, so we need to find the length of the hypotenuse using Pythagorean's Theorem:
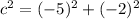 and
and
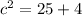 so
so
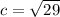
That means that
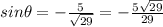 and
and
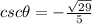
That means that
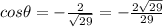 and
and
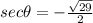
It also means that
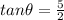 and
and
