Answer:
If
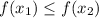 whenever
whenever
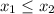 f is increasing on I.
f is increasing on I.
If
 whenever
whenever
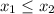 f is decreasing on I.
f is decreasing on I.
Explanation:
These are definitions for real-valued functions f:I→R. To help you remember the definitions, you can interpret them in the following way:
When you choose any two numbers
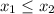 on I and compare their image under f, the following can happen.
on I and compare their image under f, the following can happen.
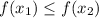 . Because x2 is bigger than x1, you can think of f also becoming bigger, that is, f is increasing. The bigger the number x2, the bigger f becomes.
. Because x2 is bigger than x1, you can think of f also becoming bigger, that is, f is increasing. The bigger the number x2, the bigger f becomes.
 . The bigger the number x2, the smaller f becomes so f is "going down", that is, f is decreasing.
. The bigger the number x2, the smaller f becomes so f is "going down", that is, f is decreasing.
Note that this must hold for ALL choices of x1, x2. There exist many functions that are neither increasing nor decreasing, but usually some definition applies for continuous functions on a small enough interval I.