Question

The local animal shelter throws a dog-themed party. Humans, h, and dogs, d are both invited. The event space imposes two restrictions on the party: there can only be 120 dogs and humans combined, and, to keep things manageable, there must be 1 human to every 3 dogs.

This situation can be represented by a system of two linear equations. One of these equations is given. Write the second equation in the box.

Answer 1

The system of equations can be expressed like

`\left\{\begin{matrix}h+d=120\\ 3h-d=0\end{matrix}\right.`

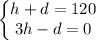
Explanation:

System of Two Linear Equations

It refers to situations where conditions are given in the form

`\left\{\begin{matrix}ax+by=c\\ dx+ey=f\end{matrix}\right.`

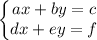
Where x and y are the unknown variables and a,b,c,d,e,f are known constants

The problem describes a situation where one event space imposes two restrictions on a dog-themed party. The first one is there can only be 120 dogs and humans combined. Being h the number of humans, and d the number of dogs, then

`h+d=120`

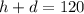
The other condition is there must be 1 human to every 3 dogs, we can model it by

`d=3h`

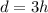
Rearranging:

`3h-d=0`

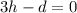
The system of equations can be expressed like

`\left\{\begin{matrix}h+d=120\\ 3h-d=0\end{matrix}\right.`

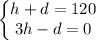
Note: The solution of the system is h=30 humans and d=90 dogs