Answer:
The system of equations can be expressed like
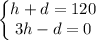
Explanation:
System of Two Linear Equations
It refers to situations where conditions are given in the form
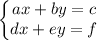
Where x and y are the unknown variables and a,b,c,d,e,f are known constants
The problem describes a situation where one event space imposes two restrictions on a dog-themed party. The first one is there can only be 120 dogs and humans combined. Being h the number of humans, and d the number of dogs, then
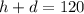
The other condition is there must be 1 human to every 3 dogs, we can model it by

Rearranging:
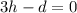
The system of equations can be expressed like
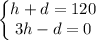
Note: The solution of the system is h=30 humans and d=90 dogs