Question

Suppose a deli sells morning newspapers at an average of 10 per hour with a standard deviation of 5. Use the Standard Normal Distribution.

a. what is the probability that the deli will sell up to 7 newspapers in a given hour?
b. What is the probability that the deli will sell 12 or more newspapers in a given hour?

Answer 1

a) 0.274 is the probability that the deli will sell up to 7 newspapers in a given hour.

b) 0.345 is the probability that the deli will sell 12 or more newspapers in a given hour.

Explanation:

We are given the following information in the question:

Mean, μ = 10 per hour

Standard Deviation, σ = 5 per hour

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

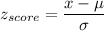
a) P(deli will sell up to 7 newspapers in a given hour)

P(x < 7)

`P( x < 7) = P( z < \displaystyle(7 - 10)/(5)) = P(z < -0.6)`

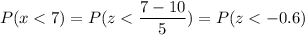
Calculation the value from standard normal z table, we have,

`P(x <7) = 0.274 = 27.4\%`

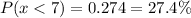
0.274 is the probability that the deli will sell up to 7 newspapers in a given hour.

b) P( deli will sell 12 or more newspapers in a given hour)

P(x > 12)

`P( x > 12) = P( z > \displaystyle(12 - 10)/(5)) = P(z > 0.4)`

`= 1 - P(z \leq 0.4)`

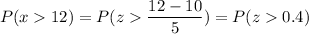
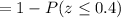
Calculation the value from standard normal z table, we have,

`P(x >12) = 1 - 0.655 = 0.345 = 34.5\%`

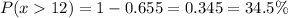
0.345 is the probability that the deli will sell 12 or more newspapers in a given hour.