Question

The long single bar on the left in the drawing has a thermal conductivity of 240 J/(s · m · °C). The ends of the bar are at temperatures of 400 and 200°C, and the temperature of its midpoint is halfway between these two temperatures, or 300°C. The two bars on the right are half as long as the bar on the left, and the thermal conductivities of these bars are different (see the drawing). All of the bars have the same cross-sectional area. What can be said about the temperature at the point where the two bars on the right are joined together?

Answer 1

To solve this problem it is necessary to apply the concepts related to the thermal transfer rate. In general, the transfer rate can be expressed as

`(Q)/(t) = (kA\Delta T)/(L)`

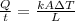
Where,

k = Thermal conductivity

A = Cross-sectional area

`\Delta T`= Change of temperature

L = Length

Since the two heat transfer rates are equivalent we have to:

`(Q_1)/(t) = (Q_2)/(t)`

`(k_1A(T_2-T_1))/(L/2)=(k_2A(T_1-T_2'))/(L/2)`

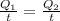
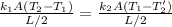
Replacing we have,

`k_1(400-T) = k_2(T-200)`

`k_1(400)-k_1T=k_2T-k_2(200)`

`k_1(400)+k_2(200)=(k_1+k_2)T`

`T = (k_1(400)+k_2(200))/(k_1+k_2)`

`T = ((240)(400)+(120)(200))/(240+120)`

`T = 333.3°C`

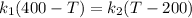
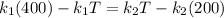
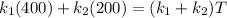
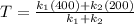
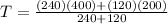
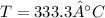
Therefore the temperature where the two bars are joined together is 300°C