To solve this problem it is necessary to apply the concepts related to the thermal transfer rate. In general, the transfer rate can be expressed as
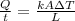
Where,
k = Thermal conductivity
A = Cross-sectional area
 = Change of temperature
= Change of temperature
L = Length
Since the two heat transfer rates are equivalent we have to:
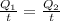
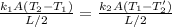
Replacing we have,
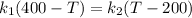
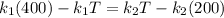
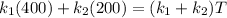
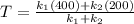
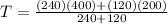

Therefore the temperature where the two bars are joined together is 300°C