To solve this problem, it is necessary to apply the concepts related to the change of entropy in function of the Volume in two states due to the number of moles and the ideal gas constant, this can be expressed as
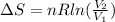
Where,
R = Gas constant
V = Volume (at each state)
At the same time the number of moles of gas would be determined by the ideal gas equation, that is,
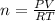
Where,
P = Pressure
V = Volume
R = Gas Constant
T = Temperature
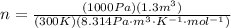

Using the value of moles to replace it in the first equation we have
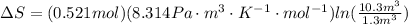
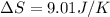
Therefore the correct option is A.