Question

A monatomic ideal gas in equilibrium at a pressure of 3 kPa and a temperature of 300 K is initially confined in a volume of 1.3 m^3 by a wall. The wall is suddenly removed and a new equilibrium state with the volume 10.4 m^3 is reached. You may assume that the system is isolated, such that there is no exchange of heat or work with its surrounding environment.1. What is the total change in entropy? a. ΔS = 9.01 J/K b. ΔS = 31.5 J/K c. ΔS = 0 J/K d. ΔS = 1.1 J/K e. ΔS = 63.1 J/K

Answer 1

To solve this problem, it is necessary to apply the concepts related to the change of entropy in function of the Volume in two states due to the number of moles and the ideal gas constant, this can be expressed as

`\Delta S = nRln((V_2)/(V_1))`

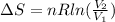
Where,

R = Gas constant

V = Volume (at each state)

At the same time the number of moles of gas would be determined by the ideal gas equation, that is,

`n = (PV)/(RT)`

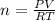
Where,

P = Pressure

V = Volume

R = Gas Constant

T = Temperature

`n = ((1000Pa)(1.3m^3))/((300K)(8.314Pa\cdot m^3\cdot K^(-1)\cdot mol^(-1)))`

`n = 0.521mol`

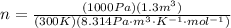
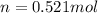
Using the value of moles to replace it in the first equation we have

`\Delta S = (0.521mol)(8.314Pa\cdot m^3\cdot K^(-1)\cdot mol^(-1))ln((10.3m^3)/(1.3m^3))`

`\Delta S = 9.01J/K`

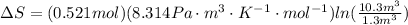
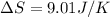
Therefore the correct option is A.