Question

Can I know the steps​

Answer 1

Explanation:

We are given:

`xy'=coty`

This can be rewritten as

`x(dy)/(dx) =coty`

Next, we can bring the x's and y's to their respective sides by dividing by coty and x and then multiplying the dx to the other side. We can then change
`(1)/(coty)` into
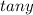`tany`. This gives us the differential

`tany\,dy=(1)/(x) \,dx`

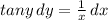
Now we can integrate each side

`\int tan(y)\,dy=\int (1)/(x) \,dx`

To integrate tan(y), we need to manipulate it

`\int (sin(y))/(cos(y)) \,dy=\int (1)/(x) \,dx`

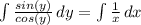
Now we can use u-substitution where
`u= cos(y)\\du=-sin(y) dy`

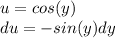
This gives us

`-\int (1)/(u) \,du=\int (1)/(x) \,dx`

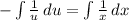
Now, lets integrate both sides

`-ln|u|=ln|x|+c`

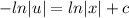
Next, we can substitute our u value back in

`-ln|cos(y)|=ln|x|+c`

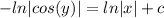
Now we can add
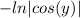`-ln|cos(y)|` to the other side and subtract c from each side. This gives us

`C_2=ln|x|+ln|cos(y)|`

Next, we can apply a property of logarithms to combine this sum of two logs into one log.

`C_2=ln|xcos(y)|`

Lastly, we can add a base e to each side to remove the ln

`C_3=|xcos(y)|`

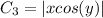
And here is our answer.