Answer:
1) x= -3, 3, 6
2) x= -3, -2, 0
Explanation:
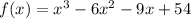
To factor this, we can use grouping
First we can factor the first pair and second pairs of terms
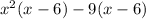
As we have the same factor on each of these, we can combine the like terms to get
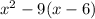
This can be factored into

This gives us the zeroes of
x= -3, 3, 6

To factor this one, we first need to factor out a term
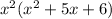
This is a quadratic equation that simplifies to
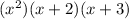
This gives the zeroes of
x= -3, -2, 0