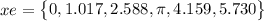Note: It's not clear if the expressions involving '2x' actually mean squaring the tangent/secant or doubling the angle x. I'm posting the answer assuming the latest approach.
Answer:
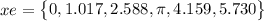
Explanation:
Trigonometric Equations
It's a type of equations where the variable is the argument of some of the trigonometric functions. It's generally restricted to a given domain, so the solution must be iteratively selected within all the possible answers.
The equation to solve is
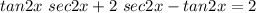
Rearranging
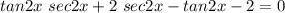
Factoring
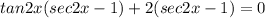
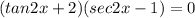
We come up with two different equations:
![\displaystyle \left\{\begin{matrix}tan2x+2=0....[eq1]\\sec2x-1=0....[eq2]\end{matrix}\right.](https://img.qammunity.org/2020/formulas/mathematics/college/x3czvjqq10d018dsbn4hz0644zyunvptlq.png)
Let's take eq 1:
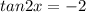
Solving for 2x
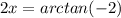
There are two sets of possible solutions:
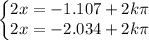
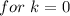
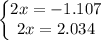
We get two solutions
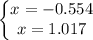 .
.
The first solution is out of the range
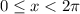 , so it's discarded
, so it's discarded
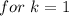
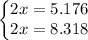 .
.
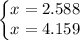 .
.
Both solutions are feasible
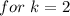
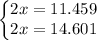 .
.
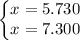 .
.
Only the first solution lies in the given domain. We won't take negative values of k since it will provide negative values of x and they are not allowed in the solution
Now we solve eq 2:

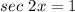
This leads to the solution
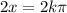
Or equivalently
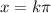
For k=0, x=0. This solution is valid
For k=1,
 . This is also valid
. This is also valid
For k=2,
 . This solution is out of range
. This solution is out of range
The whole set of solutions is