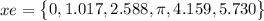Question

Find all solutions of each equation on the interval 0 ≤ x<2π.

tan2x sec2x + 2sec2x – tan2x = 2

Answer 1

`x = 0 \: or \:x = \pi`

Explanation:

The given equation is

`\tan^(2) (x) \sec^(2) (x) + \sec^(2) (x) - \tan^(2) (x) = 2`

Subtract 2 from both sides and factor by grouping to get:

`\sec^(2) (x)(\tan^(2) (x) + 2) -1( \tan^(2) (x) + 2)`

`(\tan^(2) (x) + 2) (\sec^(2) (x) - 1) = 0`

By the zero product principle:

`(\tan^(2) (x) + 2) = 0 \: or \: (\sec^(2) (x) - 1) = 0`

`(\tan^(2) (x) = - 2 \: or \: \sec^(2) (x) = 1`

When

`\sec^(2) (x) = 1 \implies\cos^(2) (x) = 1`

`\implies \: \cos(x) = \pm1`

This implies

`x = 0 \: or \:x = \pi`

When

`{ \tan }^(2) (x) = - 2`

We have

`\tan(x) = \pm √( - 2)`

hence x is not defined for all real numbers

Answer 2

Note: It's not clear if the expressions involving '2x' actually mean squaring the tangent/secant or doubling the angle x. I'm posting the answer assuming the latest approach.

Answer:

`\displaystyle xe=\begin{Bmatrix}0,1.017,2.588,\pi ,4.159,5.730\end{Bmatrix}`

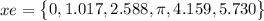
Explanation:

Trigonometric Equations

It's a type of equations where the variable is the argument of some of the trigonometric functions. It's generally restricted to a given domain, so the solution must be iteratively selected within all the possible answers.

The equation to solve is

`\displaystyle tan2x\ sec2x+2\ sec2x-tan2x=2`

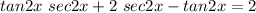
Rearranging

`\displaystyle tan2x\ sec2x+2\ sec2x-tan2x-2=0`

Factoring

`\displaystyle tan2x( sec2x-1)+2 (sec2x-1)=0`

`\displaystyle (tan2x+2)(sec2x-1)=0`

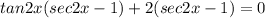
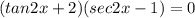
We come up with two different equations:

`\displaystyle \left\{\begin{matrix}tan2x+2=0....[eq1]\\sec2x-1=0....[eq2]\end{matrix}\right.`

Let's take eq 1:

`\displaystyle tan2x=-2`

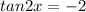
Solving for 2x

`\displaystyle 2x=arctan(-2)`

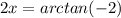
There are two sets of possible solutions:

`\left\{\begin{matrix} 2x=-1.107+2k\pi \\ 2x=-2.034+2k\pi \end{matrix}\right.`

`\displaystyle for\ k=0`

`\displaystyle \left\{\begin{matrix}2x=-1.107\\ 2x=2.034\end{matrix}\right`

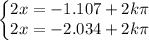
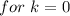
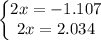
We get two solutions

`\displaystyle \left\{\begin{matrix}x=-0.554\\ x=1.017\end{matrix}\right`.

The first solution is out of the range
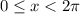`0\leq x < 2\pi`, so it's discarded

`\displaystyle for\ k=1`

`\displaystyle \left\{\begin{matrix}2x=5.176\\ 2x=8.318\end{matrix}\right`.

`\displaystyle \left\{\begin{matrix}x=2.588\\x=4.159\end{matrix}\right`.

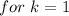
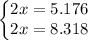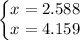Both solutions are feasible

`\displaystyle for\ k=2`

`\displaystyle \displaystyle \left\{\begin{matrix}2x=11.459\\ 2x=14.601\end{matrix}\right`.

`\displaystyle \displaystyle \left\{\begin{matrix}x=5.730\\ x=7.300\end{matrix}\right`.

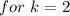
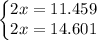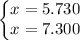Only the first solution lies in the given domain. We won't take negative values of k since it will provide negative values of x and they are not allowed in the solution

Now we solve eq 2:

`\displaystyle sec\ 2x-1=0`

`\displaystyle sec\ 2x=1`

This leads to the solution

`\displaystyle 2x=2k\pi`

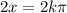
Or equivalently

`x=k\pi`

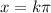
For k=0, x=0. This solution is valid

For k=1,
`x=\pi` . This is also valid

For k=2,
`x=2\pi` . This solution is out of range

The whole set of solutions is

`\displaystyle xe=\begin{Bmatrix}0,1.017,2.588,\pi ,4.159,5.730\end{Bmatrix}`