Answer:
- ∠1≅∠2-------------------------(Given)
- m∠1=m∠2-------------------(Definition of congruent angles)
- ∠ABP, ∠1 and ∠DCP,∠2 form linear pair---------------Linear pair
- m∠ABP+m∠1=180° and m∠DCP+m∠2=180°--------definition of linear pair
- ∠ABP≅∠DCP--------------------If equals are subtracted from equals, the remainders are equal
- AP≅DP----------------------------Given
- ΔABP≅ΔDCP-------------------AAS
Explanation:
Given, ∠1≅∠2, ∠3≅∠4 and AP≅DP,
∠1≅∠2(given)
⇒m∠1=m∠2(definition of congruent angles)
- ∠
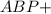 m∠1=180° and ∠
m∠1=180° and ∠
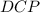 +m∠2=180° (Linear Pair)
+m∠2=180° (Linear Pair)
180°=180°(Reflexive)
⇒m∠
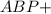 m∠1=m∠
m∠1=m∠
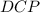 +m∠2
+m∠2
But m∠1 =m∠2 (definition of congruent angles)
⇒m∠
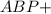 m∠1=m∠
m∠1=m∠
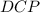 +m∠1
+m∠1
m∠
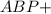 =m∠
=m∠
![DCP[/tex</strong>] ( If equals are subtracted from equals, the remainders are equal)</p><ul><li><strong>[tex]AP](https://img.qammunity.org/2020/formulas/mathematics/middle-school/75t6n3lyfjreprhkz92uwpqei1zkdtvnx8.png) =
=
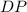 (GIven)
(GIven)
Therefore, Δ
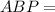 Δ
Δ
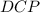 (by AAS criteria)
(by AAS criteria)
condition are:
- m∠1=m∠2 (Angle)
- m∠
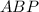 =m∠
=m∠
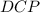 (Angle)
(Angle) - AP=DP (Side)