Answer:
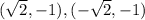
(StartRoot 2 EndRoot, negative 1) and (negative StartRoot 2 EndRoot, negative 1)
Explanation:
we have
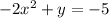 ----> equation A
----> equation A
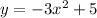 -----> equation B
-----> equation B
solve by substitution
substitute equation B in equation A
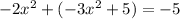
solve for x
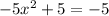
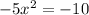
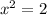
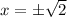
Find the value of y
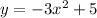
For
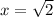 ---->
---->
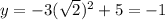
For
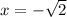 ---->
---->
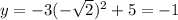
therefore
The solutions are
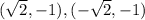
(StartRoot 2 EndRoot, negative 1) and (negative StartRoot 2 EndRoot, negative 1)