Question

Consider the function f(x) = x^3 - 15x^2 + 50x.? What are the real zeros in this function?

Answer 1

We have

`f(x)=x^3-15x^2+50x`.

To find zeros of this function we equate it with 0

`x^3-15x^2+50x=0`.

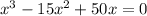First we factor out x

`x(x^2-15x+50)=0`

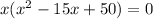
where we find that first zero is
`\boxed{x_1=0}`.

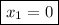Then we look at the expression in parentheses

`x^2-15x+50=0`

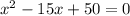
using Viéts rule (factorisation)

`(x+a)(x+b)=x^2+x(a+b)+ab`

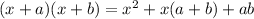
we can rewrite the equality

`(x-10)(x-5)=0`.

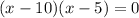If either of the terms is zero then the equality is true so we get two more zeros
`\boxed{x_2=10}` and
`\boxed{x_3=5}`.

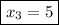Hope this helps.