Answer:
t = 186.2 μs
Step-by-step explanation:
Current in LR series circuit
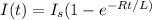 ----(1)
----(1)
steady current = I_{s} = V/R
time constant = τ =
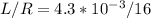
= 0.268 ms
magnetic energy stored in coil =
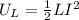
rate at which magnetic energy stored in coil=
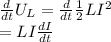 ----(2)
----(2)
rate at which power is dissipated in R:
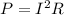 ---(3)
---(3)
To find the time when the rate at which energy is dissipated in the coil equals the rate at which magnetic energy is stored in the coil equate (2) and (3)
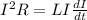
[/tex]I=\frac{L}{R}\frac{dI}{dt}[/tex]----(4)
differentiating (1) w.r.to t
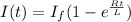

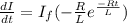 ---(5)
---(5)
substituting (5) in (4)
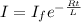 ----(6)
----(6)
equating (1) and (6)

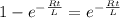
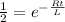
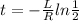
L= 4.3 mH
R= 16 Ω
t = 186.2 μs