Question

In a certain industrial process involving a heterogeneous catalyst, the volume of the catalyst (in the shape of a sphere) is 10.0 cm^3. If the sphere were broken down into eight spheres each having a volume of 1.25 cm^3, and the reaction is run a second time, which of the following accurately characterizes the second run?

Choose all that apply.
A. The second run will be faster.
B. The second run will be slower.
C. The second run will have the same rate as the first.
D. The second run has twice the surface area.
E. The second run has eight times the surface area.
F. The second run has 10 times the surface area.

Answer 1

D

Step-by-step explanation:

We know that the

reaction catalyzing power of a catalyst ∝ surface area exposed by it

Given

volume V1= 10 cm^3

⇒
`(4)/(3) \pi r^3= 10`

hence r= 1.545 cm

also, surface area S1=
`4\pi r^2`

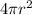
now when the sphere is broken down into 8 smaller spheres

S2= 8×4πr'^2

now, equating V1 and V2 ( as the volume must remain same )

`(4)/(3)\pi r^3=8*(4)/(3) \pi r'^3`

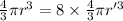
and solving we get

r'= r/2

therefore, S2=
`8*4\pi(r)/(2)^2`

S2=
`2*4\pi r^2`

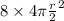
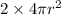
S2= 2S1

hence the correct answer is

. The second run has twice the surface area.