Answer:
D
Step-by-step explanation:
We know that the
reaction catalyzing power of a catalyst ∝ surface area exposed by it
Given
volume V1= 10 cm^3
⇒
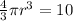
hence r= 1.545 cm
also, surface area S1=
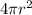
now when the sphere is broken down into 8 smaller spheres
S2= 8×4πr'^2
now, equating V1 and V2 ( as the volume must remain same )
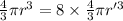
and solving we get
r'= r/2
therefore, S2=
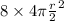
S2=
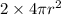
S2= 2S1
hence the correct answer is
. The second run has twice the surface area.