Question

A large fake cookie sliding on a horizontal surface is attached to one end of a horizontal spring with spring constant k = 375 N/m; the other end of the spring is fixed in place. The cookie has a kinetic energy of 19.0 J as it passes through the position where the spring is unstretched. As the cookie slides, a frictional force of magnitude 10.0 N acts on it. (a) How far will the cookie slide from the position where the spring is unstretched before coming momentarily to rest? m (b) What will be the kinetic energy of the cookie as it slides back through the position where the spring is unstretched?

Answer 1

The conservation of energy should be used to answer this question.

a)

At the position where the spring is unstretched, the elastic potential energy of the spring is zero.

`K_1 + U_1 - W_f = K_2 +U_2\\K_1 - W_f = U_2`

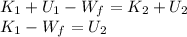
since
`U_1` and
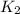`K_2` is equal to zero.

`W_f = F_fx\\\\U_2 = (1)/(2)kx^2\\\\19 - (10)x = (1)/(2)(375)x^2\\\\375x^2 + 20x - 38 = 0`

The roots of this quadratic equation can be solved by using discriminant.

`\Delta = b^2 - 4ac\\x_(1,2) = (-b \pm √(\Delta))/(2a)`

`x_1 = -0.346\\x_2 = 0.292`

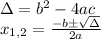
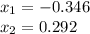
We should use the positive root, so

x = 0.292 m.

b)

We should use energy conservation between the point where the spring is momentarily at rest, and the point where the spring is unstretched.

`K_2 + U_2 - W_f = K_3 + U_3\\U_2 - W_f = K_3`

since the kinetic energy at point 2 and the potential energy at point 3 is equal to zero.

`(1)/(2)kx^2 - F_fx = K_3\\K_3 = 15.987 - 2.92 = 13.067 J`

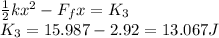
Step-by-step explanation:

In questions with springs, the important thing is to figure out the points where kinetic or potential energy terms would be zero. When the spring is unstretched, the elastic potential energy is zero. And when the spring is at rest, naturally the kinetic energy is equal to zero.

In part b) the cookie slides back to its original position, so the distance traveled, x, is equal to the distance in part a). The frictional force is constant in the system, so it is quite simple to solve part b) after solving part a).