Question

Solve the inequality and graph
2(-6n-5)<-3(4n+2)
thanks! ​

Answer 1

All real numbers are solution for the inequality.

Explanation:

Given expression:

`2(-6n-5)<-3(4n+2)`

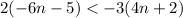
Solving the inequality.

Using the distribution.

`(2(-6n))+(-2(-5)<(-3(4n))+(-3(2))`

`-12n-10<-12n-6`

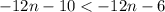
Adding
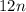`12n` to both sides.

`-12n+12n-10<-12n+12n-6`

We have,

`-10<-6`

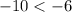
The above statement is always true and thus the inequality has all real number solutions.

The number line graph for the inequality can be shown.