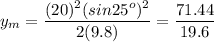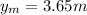Answer:
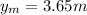
Step-by-step explanation:
Motion in The Plane
When an object is launched in free air with some angle respect to the horizontal, it describes a known parabolic path, comes to a maximum height and finally drops back to the ground level at a certain distance from the launching place.
The movement is split into two components: the horizontal component with constant speed and the vertical component with variable speed, modified by the acceleration of gravity. If we are given the values of
 and
and
 as the initial speed and angle, then we have
as the initial speed and angle, then we have
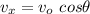
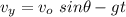
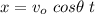
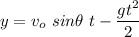
If we want to know the maximum height reached by the object, we find the value of t when
 becomes zero, because the object stops going up and starts going down
becomes zero, because the object stops going up and starts going down

Solving for t
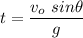
Then we replace that value into y, to find the maximum height
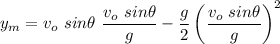
Operating and simplifying
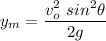
We have
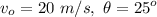
The maximum height is