Answer:
Answer is option "a" i.e.
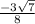
Explanation:
sin2Ф = 2sinФ.cosФ
So, we need values of sinФ and cosФ but we are given secФ. We can find sinФ and cosФ with the help of secФ first by finding all sides of triangle and then by using Pythagorean theorem.
Given that,
secФ = -4/3
While,
secФ = hypotenuse/base
Hence,
length of hypotenuse = 4
length of base = 3
To find perpendicular we'll use Pythagorean theorem:
(hyp)² = (base)² + (perp)²
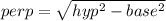

length of perpendicular = √7
Now, to find sinФ and cosФ
sinФ = perp/hyp
sinФ = √7/4
cosФ = base/hyp
cosФ = 3/4
Finally to find sin2Ф
sin2Ф = 2sinФ.cosФ
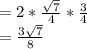
negative sign of sin2Ф
As 90≤Ф≤180
So multiplying it by 2
180≤Ф≤360
which is 3rd and 4th coordinate in which sin has negative value.