Question

An investment is advertised as returning 3.7% every 6 months (semiannually), compounded semiannually. If $50,000 is invested, the growth can be modeled by the equation A(t) = 50,000(1.037)2t.

What is the equivalent annual growth rate for this investment (rounded to the nearest hundredth of a percent) and what is it worth (rounded to the nearest thousand dollar) after 25 years?
8.50% and $308,0007.54% and $308,0007.44% and $298,00022.22% and $96,000

Answer 1

7.54% and $308,000

Step-by-step explanation:

Part 1 : Since, the amount formula in compound interest,

`A=P(1+(r)/(n))^(nt)`

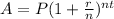
Where,

P = principal value,

r = annual rate,

n = number of compounding periods in a year,

t = number of years,

If P = $ 50,000, n = 1,

`A=50,000(1+r)^(t)-----(1)`

Suppose this amount is equivalent if
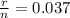`(r)/(n)=0.037` and n = 2,

Then

`50,000(1+0.037)^(2t)=50,000(1+r)^t`

`1.037^2 = 1+ r`

`1.075369-1 = r`

`\implies r = 0.075369 = 7.5369\%\approx 7.54\%`

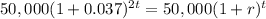
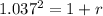
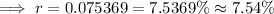
Hence, the equivalent annual growth rate for this investment would be 7.54%.

Part 2 :

If t = 25,

`A= 50,000(1+0.075369 )^(25)=307544.40\approx \$ 308,000`

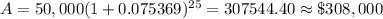
( Using calculator )

i.e. it would be worth $ 308,000( approx) after 25 years.