Answer:
The hang time is 2.04 seconds
Step-by-step explanation:
2-D Motion
It referred to as a situation where an object is launched in such a way it describes a curve, reaches a top height and then returns to ground level after traveling a certain distance x away from the launch point.
Let
 be the launching speed forming an angle
be the launching speed forming an angle
 with the horizontal reference. The hang time (time the object remains in the air) is given by
with the horizontal reference. The hang time (time the object remains in the air) is given by

Since
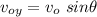
Then
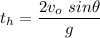
We'll use the given values
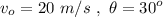
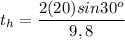
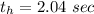
The hang time is 2.04 seconds