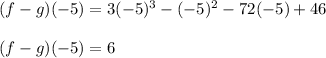Question

A: Given f(x) = x^2 + 16 - 24 and g(x) = x^2 - 5x - 17, find (f+g)(x), then find (f+g)(3)

(possible answers for (f+g)(3): 2x^2 + 11x - 41 OR 2x^2 + 11x - 7)


B: Given f(x) = 4x^3 - x^2 - 68x + 35 and g(x) = x^3 + 4x - 11, find (f - g)(x), Then find (f - g)(-5)

(Possible answers for (f-g)(-5): 3x^3 - x^2 - 72x + 46 OR 3x^3 - x^2 -64x +24)


PLEASE SHOW WORK IF POSSIBLE FOR YOU :)

Answer 1

`A.\ (f+g)(x) =2x^2+11x-41\\\\ (f+g)(3) =10\\\\\\ B.\ (f-g)(x)=3x^3-x^2-72x+46\\\\ (f-g)(-5)=6`

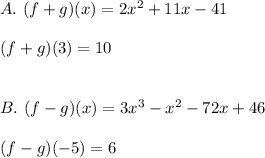
Explanation:

A. Knowing that the functions are:

`f(x) = x^2 + 16x - 24\\\\g(x) = x^2 - 5x - 17`

You need to add them in order to find
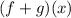`(f+g)(x)`. Then, you get:

`(f+g)(x) = x^2 + 16x - 24+x^2 - 5x - 17\\\\(f+g)(x) =2x^2+11x-41`

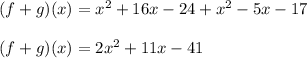
To find:

`(f+g)(3)`

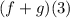
Substitute
`x=3` into
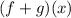`(f+g)(x)` and evaluate.

Then, this is:

`(f+g)(3) =2(3)^2+11(3)-41\\\\(f+g)(3) =10`

B. The functions f(x) and g(x) are:

`f(x) =4x^3 - x^2 - 68x + 35\\\\g(x) = x^3 + 4x - 11`

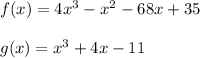
You need to subtract them in order to find
`(f-g)(x)`:

`(f-g)(x) = 4x^3 - x^2 - 68x + 35-(x^3 + 4x - 11)\\\\(f-g)(x) =4x^3 - x^2 - 68x + 35-x^3 -4x +11\\\\(f-g)(x)=3x^3-x^2-72x+46`

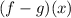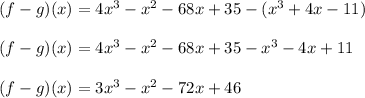
To find:

`(f-g)(-5)`

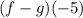
Substitute
`x=-5` into
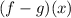`(f-g)(x)` and evaluate.

Then, this is:

`(f-g)(-5)=3(-5)^3-(-5)^2-72(-5)+46\\\\(f-g)(-5)=6`