To solve this problem it is necessary to apply dynamic similarity relationships from the Reynolds model, for which you have the relationship
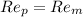

Where,
 = Density
= Density
V = Velocity
D = Diameter
\mu = Dynamic viscosity
Here the number p refers to the scale model, that is the prototype and m refers the real model.
For the conditions presented we have through the properties of gases (air for this case) in query tables that:
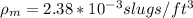
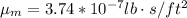
From the properties of fluids (water) we have that the scale model properties would be
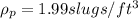
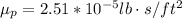
Substituting the values given in the equation we have to,

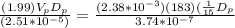
The term of the diameter is eliminated on both sides so the speed for the prototype would be:
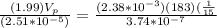
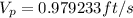
Therefore the speed of the prototype to ensure Reynolds number similarity is 0.979233ft/s