Question

The ratio of the volume of soda in glass A to the volume of glass B is 8/3 to 7/2

If there is 320mL of soda in glass A, what is the total volume in the two glasses

Answer 1

Total volume in two glasses is 740 ml

Solution:

Given that ratio of the volume of soda in glass A to the volume of glass B is 8/3 to 7/2

There is 320mL of soda in glass A

To find: total volume in the two glasses

From given information,

volume of soda in glass A : volume of soda in glass B =
`(8)/(3) : (7)/(2)`

Ratio a : b can be written in fraction as
`(a)/(b)`

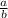
Similarly,

`\frac{\text {volume of soda in glass } A}{\text {volume of soda in glass } B}=(8 / 3)/(7 / 2)`

`\frac{\text {volume of soda in glass } A}{\text {volume of soda in glass } B}=((8)/(3))/((7)/(2))=(8)/(3) * (2)/(7)`

`\frac{\text {volume of soda in glass } A}{\text {volume of soda in glass } B}=(16)/(21)`

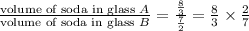
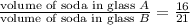
Given that There is 320mL of soda in glass A

So substituting in above equation,

`\frac{320}{\text { volume of soda in glass } B}=(16)/(21)`

`\text {volume of soda in } g \text {lass } B=320 * (21)/(16)=420`

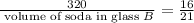
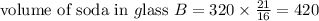
Thus volume of soda in glass B = 420 ml

Total volume in two glasses:

total volume in the two glasses = volume of soda in glass A + volume of soda in glass B

total volume in the two glasses = 320 ml + 420 ml = 740 ml

Thus total volume in two glasses is 740 ml