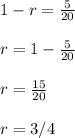Answer:
- The common ratio of the progression is 3/4
Step-by-step explanation:
A geometric progression is a sequence of terms in which the consecutive terms have a constant ratio; thus, each term is equal to the previous one multiplied by a constant value:
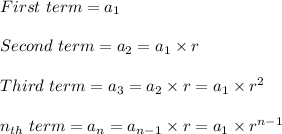
A infinite geometric progression may have a finite sum. When the absolute value of the ratio is less than 1, the sum of the infinite geometric progression has a finite value equal to:
Thus, the information given translates to:
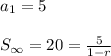
Now you can solve for the constant ratio, r: