Answer: c. -2.15
Explanation:
As per given we have:
Null hypothesis :
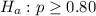
Alternative hypothesis :
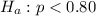
let p be the proportion of firms in the manufacturing sector offer child-care benefits
A random sample of 390 manufacturing firms is selected and 295 of them offered child-care benefits.
sample size : n= 390
sample proportion :
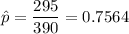
Test statistic for proportion :
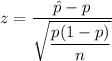
Substitute the values , we get
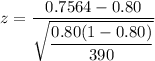

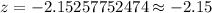
Hence, the value of test statistic = -2.15
Correct option is c. -2.15 .