Question

Given a function
`f(x)=3x^4-5x^2+2x-3`, evaluate
`f(-1)`

Answer 1

f(-1) = -7

Explanation:

f(x) = 3x^4 - 5x^2 +2x -3

Let x = -1

f(-1) = 3 ( -1)^4 - 5(-1)^2 +2(-1) -3

Using the order of operations, do exponents first

f(-1) = 3 ( 1) - 5(1) +2(-1) -3

Then multiply

f(-1) = 3 - 5 -2 -3

Then add and subtract

f(-1) = -7

Answer 2

`\huge\boxed{f(-1) = -7}`

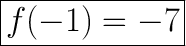
Explanation:

In order to solve for this function, we need to substitute in our value of x inside to find f(x). Since we are trying to evalue f(-1), we will substitute -1 in as x to our equation.

`f(-1) = 3(-1)^4 - 5(-1)^2 + 2(-1) - 3`

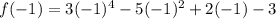
Now we can solve for the function by multiplying/subtracting/adding our known values.

Starting with the first term to the last term:

• 
  `3(-1)^4 = 3`

WAIT! How is this possible?
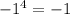`-1^4 = -1` (according to my calculator), and
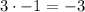`3 \cdot -1 = -3`, not 3!

It's important to note that taking a power of a negative number and multiplying a negative number are two different things. Let's use
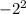`-2^2` as an example.

What your calculator did was follow BEMDAS since it wasn't explicitly told not to.

BEMDAS:

- Brackets

- Exponents

- Multiplication/Division

- Addition/Subtraction

Examining the equation, your calculator used this rule properly. Note that exponents come over multiplication.

So rather than being "-2 squared" - it's "the negative of of 2 squared."

Tying this back into our problem, the squared method would only be true if it looks like
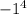`-1^4`. However, since we're substituting in -1, it looks like
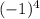`(-1)^4`, so the expression reads out as "-1 to the fourth."

MULTIPLYING -1 by itself 4 times results in
`-1\cdot-1\cdot-1\cdot-1=1`.

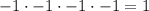Applying this logic to our original term,
`3(-1)^4`:

• 
  `3(-1\cdot-1\cdot-1\cdot-1)`
• 
  `3(1)`
• 
  `3`

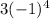Therefore, our first term is 3.

Let's move on to our second and third terms.

Second term:
`-5x^2`

• 
  `-5(-1)^2`

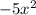
Applying the same logic from our first term:

• 
  `-5(-1 \cdot -1)`
• 
  `-5(1)`
• 
  `-5`

Third term:
`2x`

• 
  `2(-1) = -2`

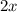
-3 is just -3, no influence of x.

Combining our terms, we have
`3-5-2-3`.

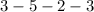This comes out to be -7, hence, the value of
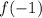`f(-1)` for our function
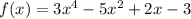`f(x)=3x^4-5x^2+2x-3` is -7.

Hope this helped!