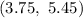Question

Georgianna claims that in a small city renowned for its music school, the average child takes at least 5 years of piano lessons. We have a random sample of 20 children from the city, with a mean of 4.6 years of piano lessons and a standard deviation of 2.2 years. What is the 90% confidence interval for the average number of years students take piano lessons in this city?

Answer 1

Answer:
`(3.75,\ 5.45)`

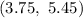
Explanation:

Given : Sample size of children : n= 20

Degree of freedom = df =n-1 =20-1=19

Sample mean years of piano lessons :
`\overline{x}=4.6`

Sample standard deviation :
`s= 2.2`

Confidence level :
`1-\alpha= 0.90`

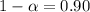
Significance level :
`\alpha= 1-0.90=0.10`

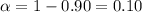
Since population standard deviation is unavailable, then

Confidence interval for the population mean :

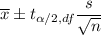`\overline{x}\pm t_(\alpha/2, df)(s)/(√(n))` (1)

Using t-distribution table , we have

Critical value =
`t_(\alpha/2, df)=t_(0.05 , 19)=\pm1.7291`

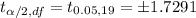
The 90% confidence interval for the average number of years students take piano lessons in this city will be :

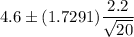`4.6\pm (1.7291)(2.2)/(√(20))` (Substitute the values in (1))

`4.6\pm (1.7291)(0.491935)`

`\approx4.6\pm 0.85`

`(4.6- 0.85,\ 4.6+ 0.85)`

`(3.75,\ 5.45)`

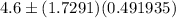
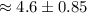
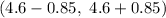
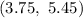
Hence, the 90% confidence interval for the average number of years students take piano lessons in this city =
`(3.75,\ 5.45)`