Answer:

Explanation:
Area Of A Cube
Suppose a cube with side length s, the area of one side is
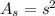
Since the cube has 6 sides, the total area is
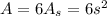
But if we have the area, we can solve the above formula for s to get
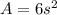
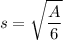
We have two different cubes with areas 1,200 square inches and 768 square inches. Let's compute their side lengths
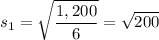

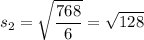
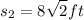
The difference between them is
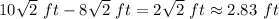
The side of the cube with area 1,200 square inches is
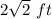 longer then the side of the cube with area 768 square inches
longer then the side of the cube with area 768 square inches