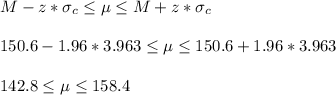Answer:
95% Confidence interval for the mean
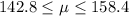
Explanation:
We have to calculate a 95% confidence interval for the mean of a finite population.
The error is multiplied by the following finite population correction factor:
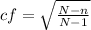
The standard deviation can be estimated as

The 95% confidence interval has a z value of 1.96, so it becomes: