Question

A hypodermic needle can be thought of as a large area pipe leading to a small pipe that opens into the vein. The diameter of the plunger is 1.2 cm and the needle diameter is 0.15 cm. If the gauge pressure in the vein is 25 mmHg, what minimum is needed on the plunger in order for a fluid flow into the vein to occur

Answer 1

According to the statement and the data presented, it is presumed that the variable to look for is force. To solve this problem it is necessary to apply the concepts related to the Force according to the pressure and the Area.

Mathematically the Force can be expressed as

`F = PA`

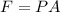
Where,

P = Pressure (At this case, the plunger pressure)

A = Cross-sectional Area ( At this case the plunger area), defined for a circle.

Our values are given as,

`r = 0.006m`

`P = 25mmHg`

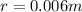
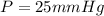
Replacing we have that

`F = (25mmHg \big [(133N/m^2)/(1mm\cdot Hg) \big ])(\pi 0.006^2)`

`F = 0.376N`

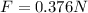
Therefore the minimum force needed on the plunger inorder for a fluid flow into the vein to occur is 0.376