Question

The initial kinetic energy imparted to a 0.020 kg bullet is 1200 J. (a) Assuming it

accelerated down a 1.00 m rifle barrel, estimate the average power delivered to it during
the firing. (b) Neglecting air resistance, find the range of this projectile when it is fired
at an angle such that the range equals the maximum height attained.

Answer 1

(a) Power= 207.97 kW

(b) Range= 5768.6 meter

Step-by-step explanation:

Given,

Mass of bullet,
`m=0.02 kg`

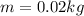
Kinetic energy imparted,
`K=1200 J`

Length of rifle barrel,
`d=1 m`

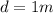
(a)

Let the speed of bullet when it leaves the barrel is
`v`.

Kinetic energy,
`K=(1)/(2) mv^(2)`

`v=\sqrt{(2K)/(m) }`

`=\sqrt{(2*1200)/(0.02) }`

`=346.4m/s`

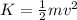
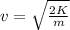
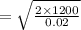
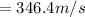
Initial speed of bullet,
`u=0`

The average speed in the barrel,
`v_a_v_g=(u+v)/(2)`

`=(0+346.4)/(2) \\=173.2 m/s`

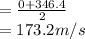
Time taken by bullet to cross the barrel,
`t=(d)/(v)`

`=(1)/(173.2)\\ =0.00577 second`

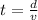
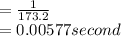
Power,
`P_a_v_g=(W)/(t)`

`=(1200)/(0.00577) \\=207.97kW`

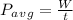
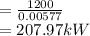
(b)

In projectile motion,

Maximum height,
`H_m=(v^2\sin^2\theta)/(2g) \\`

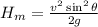
Range,
`R=(v^2\sin2\theta)/(g)`

given that,
`H_m=R`

then,
`(v^2\sin^2\theta)/(2g)=(v^2\sin2\theta)/(g)\\\sin^2\theta=2\sin\theta\cos\theta\\\\\tan\theta=4\\\theta=\tan^-^14\\\theta=75.96^0\\R=(v^2\sin2\theta)/(g)\\=(346.4^2*\sin(2*75.96))/(9.8)\\5768.6 meter`