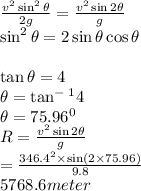Answer:
(a) Power= 207.97 kW
(b) Range= 5768.6 meter
Step-by-step explanation:
Given,
Mass of bullet,
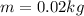
Kinetic energy imparted,
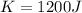
Length of rifle barrel,
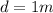
(a)
Let the speed of bullet when it leaves the barrel is
 .
.
Kinetic energy,
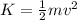
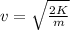
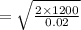
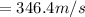
Initial speed of bullet,
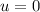
The average speed in the barrel,
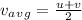
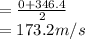
Time taken by bullet to cross the barrel,
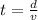
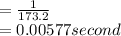
Power,
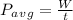
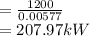
(b)
In projectile motion,
Maximum height,
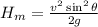
Range,
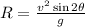
given that,
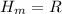
then,