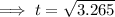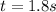Question

A ball is droped from a height of 16m how much time will pass before the ball hits the ground​

Answer 1

The time is 1.8s

Step-by-step explanation:

The ball droped, will freely fall under gravity.

Hence we use free fall formula to calculate the time by the ball to hit the ground

`h= (1)/(2)g{t}^(2)`

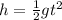
Where h is the height from which the ball is droped, g is the acceleration due to gravity that acted on the ball, and t is the time taken by the ball to hit the ground.

From the question,

h=16m

Also, let take

`g = 9.8m{s}^(-2)`

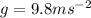
By substitution we obtain,

`16= (1)/(2)* 9.8{t}^(2)`

`\implies32=9.8{t}^(2)`

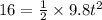
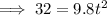
Diving through by 9.8

`(32)/(9.8)= \frac{ 9.8{t}^(2) }{9.8}`

`\implies{t}^(2) =3.265`

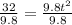
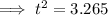
square root both sides, we obtain

`\implies t= √(3.265)`

`t=1.8s`