Question

A motorboat travels 220 kilometers in 4 hours going upstream. It travels 260 kilometers going downstream in the same amount of time. What is the rate of the boat in still water and what is the rate of the current? Rate of the boat in still water: kmh Rate of the current: kmh

Answer 1

Answer: The rate of boat is 60 kmh.

The rate of current is 5 kmh.

Explanation:

Alright, lets get started.

Suppose the rate of boat in still water is : b kmh

Suppose the rate of current is : c kmh

When the boat is going upstream, the relative speed will be :
`(b-c)`

When the boat is going downstream, the relative speed will be:
`(b+c)`

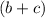
Boat travels 220 kilometers in 4 hours going upstream.

`speed=(distance)/(time)`

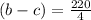`(b-c)=(220)/(4)` .................. equation (1)

It travels 260 kilometers going downstream in the same amount of time.

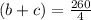`(b+c)=(260)/(4)` ................... equation (2)

Adding equation 1 and 2

`b-c+b+c=(220)/(4)+(260)/(4)`

`2b=(480)/(4)`

`2b=120`

`b=60`

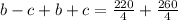
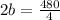
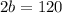
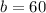
Plugging the value of b as 60 in equation 2

`60+c=(260)/(4)`

`60+c=65`

`c=5`

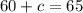
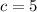
Hence the rate of boat is 60 kmh.

Hence the rate of current is 5 kmh.

Hope it will help :)