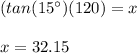Question

A street slopes upward at an angle of 15o with the horizontal. How high does it rise over a horizontal distance of 120 meters? Explain the thinking you use to arrive at your answer.

Answer 1

Answer:
`32.15\ meters`

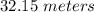
Explanation:

You can draw a right triangle (Observe the figure attached. It is not drawn to scale), where "x" is the the amount of meters the street rises over a horizontal distance of 120 meters.

You need to use the following Trigonometric Identity:

`tan\alpha=(opposite)/(adjacent)`

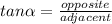
In this case, you can identify that:

`\alpha=15\°\\\\opposite=x\\\\adjacent=120`

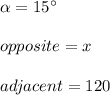
Then, knowing these values, you can substitute them into
`tan\alpha=(opposite)/(adjacent)`:

`tan(15\°)=(x)/(120)`

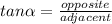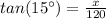
And finally, you must solve for "x" in order to find its value.

You get this result:

`(tan(15\°)(120)=x\\\\x=32.15`