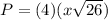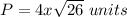The lengths of the diagonals of a rhombus are 2x and 10x. What expression gives the perimeter of the rhombus? A. 42 B. 196

Question

asked Jul 11, 2020 52.9k views

1 Answer

Hargo · Answer 1 · 2020-07-15T21:17:09+0000

Answer:

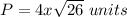
$P=4x√(26)\ units$

Explanation:

we know that

The sides of a rhombus are all congruent and the diagonals are perpendicular bisectors of each other

so

Applying the Pythagorean Theorem

c^2=a^2+b^2

where

c is the length side of the rhombus

a and b are the semi-diagonals

we have

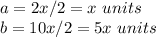
$a=2x/2=x\ units\\b=10x/2=5x\ units$

substitute the values

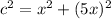
c^2=x^2+(5x)^2

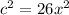
c^2=26x^2

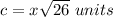
$c=x√(26)\ units$

To find out the perimeter of the rhombus multiply the length side by 4

P=(4)(x√(26))

$P=4x√(26)\ units$