Question

Find the coordinates of the other endpoint of the​ segment, given its midpoint and one endpoint.​ (Hint: Let​ (x,y) be the unknown endpoint. Apply the midpoint​ formula, and solve the two equations for x and​ y.)

midpoint ​( -4−10​), endpoint ​(2.−13​)

Answer 1

The required points of the given line segment are ( - 10, - 7 ).

Explanation:

Given that the line segment AB whose midpoint M is ( - 4, -10 ) and point A is ( 2, - 13), then we have to find point B of the line segment AB -

As we know that-

If a line segment AB is with endpoints (
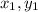`x_(1), y_(1)` ) and (
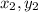`x_(2), y_(2)` )then the mid points M are-

M = (
`( x_(1) + x_(2) )/(2)` ,
`( y_(1) + y_(2) )/(2)` )

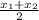Here,

Let A ( 2, - 13 ), B ( x, y ) with midpoint M ( - 4, - 10 ) -

then by the midpoint formula M are-

( - 4, - 10 ) = (
`( 2 + x)/(2)` ,
`(- 13 + y)/(2)` )

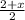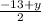On comparing x coordinate and y coordinate -

We get,

(
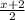`(x + 2)/(2)` = - 4 ,
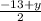`( - 13 + y)/(2)` = - 10)

( x + 2 = - 8, - 13 + y = - 20 )

( x = - 8 - 2, y = - 20 + 13 )

( x = - 10, y = - 7 )

Hence the required points A are ( - 10, - 7 ).

We can also verify by putting these points into Midpoint formula.