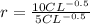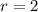Answer:
ratio of the average convection heat transfer = 2
Step-by-step explanation:
local heat transfer expression can be written as
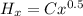 (1)
(1)
C= Constant
x=measured from the leading edge of the plate
We need to find local heat transfer coefficient at
x=5L
so for equation 1 it can be written as
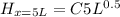
we can find the average heat transfer over entire lenght of plate as
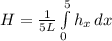 (2)
(2)
subsitute
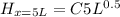 in equation 2
in equation 2
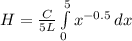
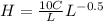

for ratio of the average convection heat transfer coefficient over the entire plate of length L to the local convection heat transfer coefficient at the end of the plate is given as

Now putting values for H ,Hx and 5L for x