Answer:
Frequency = 658 Hz
Step-by-step explanation:
The third harmonics of A is,
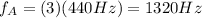
The second harmonics of E is,
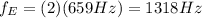
The difference in the two frequencies is,
delta_f = 1320 Hz - 1318 Hz = 2 Hz
The beat frequency between the third harmonic of A and the second harmonic of E is,
delta_f =

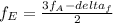
We have calculate the frequency of the E string when she hears four beats per second, then
delat_f = 4 Hz
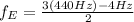
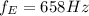
Hope this helps!