Question

Piano tuners tune pianos by listening to the beats between the harmonics of two different strings. When properly tuned, the note A should have the frequency 440 Hz and the note E should be at 659 Hz . The tuner can determine this by listening to the beats between the third harmonic of the A and the second harmonic of the E.

A tuner first tunes the A string very precisely by matching it to a 440 Hz tuning fork. She then strikes the A and E strings simultaneously and listens for beats between the harmonics. The beat frequency that indicates that the E string is properly tuned is 2.0 Hz
The tuner starts with the tension in the E string a little low, then tightens it. What is the frequency of the E string when she hears four beats per second?

Answer 1

Frequency = 658 Hz

Step-by-step explanation:

The third harmonics of A is,

`f_(A)=(3)(440Hz)=1320Hz`

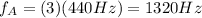
The second harmonics of E is,

`f_(E)=(2)(659Hz)=1318Hz`

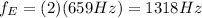
The difference in the two frequencies is,

delta_f = 1320 Hz - 1318 Hz = 2 Hz

The beat frequency between the third harmonic of A and the second harmonic of E is,

delta_f =
`3f_(A)-2f_(E)`

`f_(E)=(3f_(A)-delta_f)/(2)`

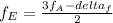
We have calculate the frequency of the E string when she hears four beats per second, then

delat_f = 4 Hz

`f_(E)=(3(440Hz)-4Hz)/(2)`

`f_(E)=658Hz`

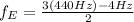
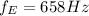
Hope this helps!