Answer:
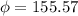
Step-by-step explanation:
from figure
taking summation of force in x direction be zero
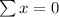
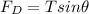 .....1
.....1
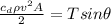
taking summation of force in Y direction be zero
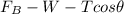
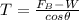 .........2
.........2
putting T value in equation 1
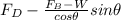
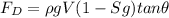 .........3
.........3
![F_D = \rho g [(\pi d^3)/(6)] ( 1 -Sg) tan \theta](https://img.qammunity.org/2020/formulas/engineering/college/l7plgjbgik6p99e012zs8jswvj6pif60bj.png)
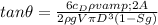
Water at 10 degree C has kinetic viscosity v = 1.3 \times 10^{-6} m^2/s
Reynold number
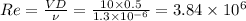
so for Re =
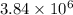 cd is 0.072
cd is 0.072
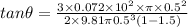
![\theta = tan^(-1) [(3* 0.072 * 10^2 * \pi * 0.5^2)/( 2* 9.81 \pi 0.5^3(1- 1.5))]](https://img.qammunity.org/2020/formulas/engineering/college/n2b34imtyrglv2w7ig2sqp532cto3hbqz3.png)
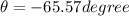
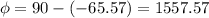 degree
degree