Question

I need answers for the problems listed below

Answer 1

(27)

• Velocity of salmon is 18m/s.

(28)

• Rocket's totle time in the air is 4.48 second.
• Rocket's maximum height is 33.58 meter.
• Rocket will land 91.6 meter away.

(29)

• Final velocity is 23.96m/s.

(30)

• (a) Peak height is 24.8 meter.

• (b) Initial angle is 23.45°.

• (c) Initial velocity is 55.4m/s

Step-by-step explanation:

Projectile Motion: When a body is launched in air at an angle
`\theta` with the horizontal with speed
`v` ,It makes a certain trajectory in influence of gravity.

Time of flight of projectile,
`T=(2v\sin\theta)/(g)`

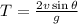
Maximum height of projectile,
`H_m=(v^2\sin^2\theta)/(2g)`

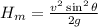
Horizontal range of projectile,
`R=(v^2\sin2\theta)/(g)`

• (27)

Given,

Distance of final position of salmon from base of cliff,
`D=90meter`

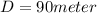
Height of cliff,
`H=122.5meter`

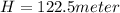
If the salmon is launched horizontally, the vertical component of velocity
`v_y` will be zero.

Using second equation of motion,

`H=v_yt-(1)/(2)gt^2 \\122.5=0-(gt^2)/(2) \\t=5second`

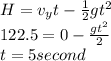
Let horizontal component of velocity is
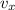`v_x`. Time taken to reach 90 meter away from base is 5 second.

So,
`v_x=(D)/(t)=(90)/(5)\\  =18second`

Hence, Velocity,
`v=v_x+v_y=0+18\\=18m/s`

• (28)

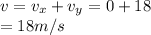
Given,

Initial velocity,
`v=30m/s`

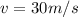
Angle,
`\theta=47^0`

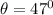
(a)

Totle time,
`T=(2v\sin\theta)/(g)\\=(2*30*\sin47^0)/(9.8)\\=4.48second`

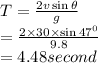
So, Rocket's totle time in the air is 4.48 second.

(b)

Maximum height,
`H_m=(v^2\sin^2\theta)/(2g)\\=(30^2*\sin^247)/(2*9.8)\\33.58meter`

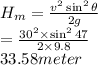
So, Rocket's maximum height is 33.58 meter.

(c)

Range,
`R=(v^2\sin2\theta)/(g)\\=(30^2\sin(2*47))/(9.8)\\ 91.6meter`

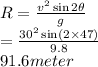
So, Rocket will land 91.6 meter away.

• (29)

Given,

Since, It started from rest, then initial velocity
`u=0`

Acceleration,
`a=7m/s^2`

Distance traveled,
`S=41meter`

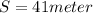
Using third equation of motion

`v^2-u^2=2as\\v=√(2as)\\=√(2*7*41)\\ =23.96m/s`

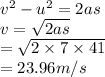
So, Final velocity is 23.96m/s.

• (30)

Given,

Range of trebuchet,
`R=225meter`

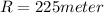
Time of flight,
`T=4.5second`

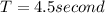
Now,

`T=(2v\sin\theta)/(g) =4.5\\v\sin\theta=(4.5*9.8)/(2) =22.05\\H_m=((v\sin\theta)^2)/(2g) =(22.5^2)/(2*9.8)=24.8meter\\(R)/(H_m)=(v^2*\sin2\theta*2*9.8)/(v^2*\sin^2\theta*9.8) =(225)/(24.8) \\\cot\theta=(225)/(24.8*4) \\\theta=23.45^0\\`

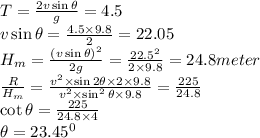
Put value
`\theta`

`(2v\sin\theta)/(g) =4.5\\v=(4.5*9.8)/(2*\sin23.45)=55.4m/s\\`

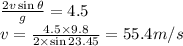
Hence

(a) Peak height is 24.8 meter.

(b) Initial angle is 23.45°.

(c) Initial velocity is 55.4m/s