Answer:
(27)
- Velocity of salmon is 18m/s.
(28)
- Rocket's totle time in the air is 4.48 second.
- Rocket's maximum height is 33.58 meter.
- Rocket will land 91.6 meter away.
(29)
- Final velocity is 23.96m/s.
(30)
- (a) Peak height is 24.8 meter.
- (b) Initial angle is 23.45°.
- (c) Initial velocity is 55.4m/s
Step-by-step explanation:
Projectile Motion: When a body is launched in air at an angle
 with the horizontal with speed
with the horizontal with speed
 ,It makes a certain trajectory in influence of gravity.
,It makes a certain trajectory in influence of gravity.
Time of flight of projectile,
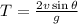
Maximum height of projectile,
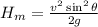
Horizontal range of projectile,
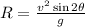
Given,
Distance of final position of salmon from base of cliff,
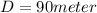
Height of cliff,
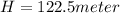
If the salmon is launched horizontally, the vertical component of velocity
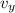 will be zero.
will be zero.
Using second equation of motion,
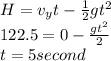
Let horizontal component of velocity is
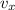 . Time taken to reach 90 meter away from base is 5 second.
. Time taken to reach 90 meter away from base is 5 second.
So,
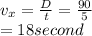
Hence, Velocity,
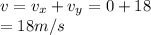
Given,
Initial velocity,
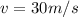
Angle,
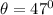
(a)
Totle time,
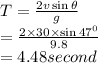
So, Rocket's totle time in the air is 4.48 second.
(b)
Maximum height,
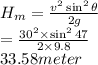
So, Rocket's maximum height is 33.58 meter.
(c)
Range,
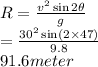
So, Rocket will land 91.6 meter away.
Given,
Since, It started from rest, then initial velocity
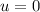
Acceleration,
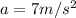
Distance traveled,
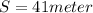
Using third equation of motion
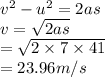
So, Final velocity is 23.96m/s.
Given,
Range of trebuchet,
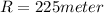
Time of flight,
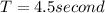
Now,
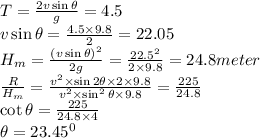
Put value

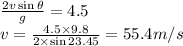
Hence
(a) Peak height is 24.8 meter.
(b) Initial angle is 23.45°.
(c) Initial velocity is 55.4m/s